网络流：最小割

将图 $G$ 分为 $A$ 和 $B$ 两个点集，$A$ 和 $B$ 之间的边的集合称为无向图的割集。带权图的割 (Cut) 就是割集中的边权之和。

S - T 最小割

特别地，对于一个网络，在满足 $源点 s \in 点集{S}, 汇点 t \in 点集{T}(S\cap T= \varnothing)$ 的情况下，从 S 到 T 的边的权值和被称为 S 到 T 的割。

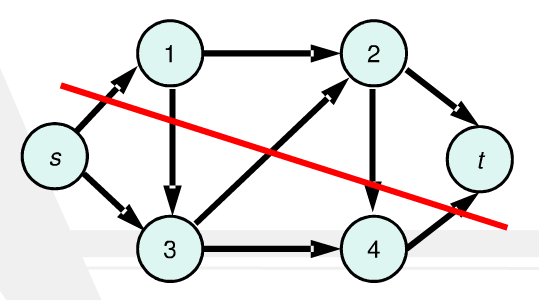
通俗地说，如果把你家和自来水厂之间的水管网络砍断了一些，那么自来水厂无论怎么放水，水都无法到达你们家，自然就停水了，砍掉的水管就是割。

砍水管的人自然希望花的力气越小越好。在所有割中，权值和最小的称为最小割。对于一个给定的 S - T 网络，如何求出它的最小割呢？

最大流最小割定理

网络的最大流等于最小割。

这个定理看起来很简单，但是真去思考的话其实挺麻烦的。

证明 Step 1：任意一个流都小于等于任意一个割

自来水公司随便给你家通点水，构成一个流，随便砍几刀砍出一个割，那么由于容量限制，每一根的被砍的水管子流出的水流量都小于管子的容量。每一根被砍的水管的水本来都要到你家的，现在流到外面，加起来得到的流量还是等于原来的流。而管子的容量加起来就是割，所以流小于等于割。

由于上面的流和割都是任意构造的，所以任意一个流小于任意一个割，即
$$
\forall F \leqslant \forall C
$$

Step 2：构造出一个流，使它等于一个割

当达到最大流时，根据增广路定理，残留网络中 s 到 t 已经没有通路了。因此，若把残余网络中 s 能到的的点的集合设为 S，不能到的点集为 T ，构造出一个割集 $C[点集S,点集T]$，所有由 S 发往 T 的边必然满流。并且，这些满流边的流量和就是当前的流，即最大流。把这些满流边作为割，就构造出了一个和最大流相等的割。

Step 3：最大流等于最小割

设上一步构造出流和割分别为 $F_m$ 和 $C_m$。

又 $\forall F \leqslant \forall C$

$\therefore \forall F \leqslant F_m=C_m \leqslant \forall C$。

网络流等价定理

综合最大流最小割定理和增广路定理，可以得到这样的结论：

对于一个网络流图 $G=(V,E)$，其中有源点 $s$ 和汇点 $t$ ，那么下面三个条件是等价的：

1. 流 $f$ 是图 $G$ 的最大流；

2. 残留网络 $G$ 不存在增广路；

3. 在 $G$ 中必存在一个割 $C[S,T]$，使得 $f=C[S,T]$。

读者自证不难

证明 1 => 2（即增广路定理）

利用反证法，假设流 $f$ 是图 $G$ 的最大流，但是残留网络中还存在有增广路 $p$，其流量为 $f_p$，则有流 $f’=f+f_p>f$。这与 $f$ 是最大流产生矛盾。

证明 2 => 3（即最大流最小割定理）

总结一下上面的证明。

假设残留网络 $G_f$ 不存在增广路，所以在残留网络 $G_f$ 中不存在路径从 $s$ 到达 $t$。我们定义 $S$ 集合为当前残留网络中 $s$ 能够到达的点，同时定义 $T=V-S$，此时构成一个割 $C(S,T)$。

且 $u∈S,v∈T$，有 $f(u,v)=c(u,v)$。若 $f(u,v)<c(u,v)$，则有 $G_f(u,v)>0$，$s$ 可以到达 $v$，与 $v \in T$ 矛盾。

因此有 $f(S,T)= \sum f(u,v)=\sum c(u,v)=C(S,T)$。

证明 3 => 1：

由于 $f$ 的上界为最小割，当 $f$ 到达割的容量时，显然就已经到达最大值，因此 $f$ 为最大流。

这样就说明了为什么找不到增广路时，所求得的一定是最大流。

最大权闭合子图

在一个图中，我们选取一些点构成集合，记为 V，且集合中的出边（即集合中的点的向外连出的弧），所指向的终点也在 V 中，则我们称 V 为闭合图。在所有闭合图中，集合中点的权值之和最大的 V，称为最大权闭合子图。

栗子

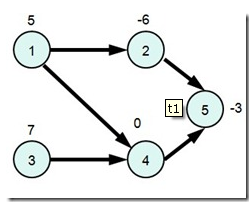
上图中最大权闭合子图为 {3,4,5}。

最大权闭合子图权值和

构图

构建一个超级源点 s，一个超级汇点 t，所有的点按权值的正负连接到 s 和 t 上，转换成一个边权值有向图，如下图：

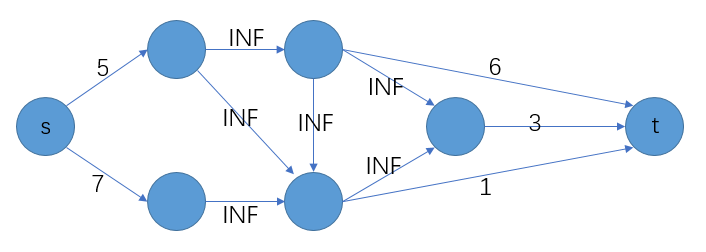
（注：点权为 0 的点可以忽略，对结果没有影响）

前置知识

• 该带边权有向图的 S - T 最小割，割集中所有的边，都与 s 或 t 相连接。

显然，因为不与 s,t 相连的边，权值都是 INF，最小割不可能割在 INF 的边上。

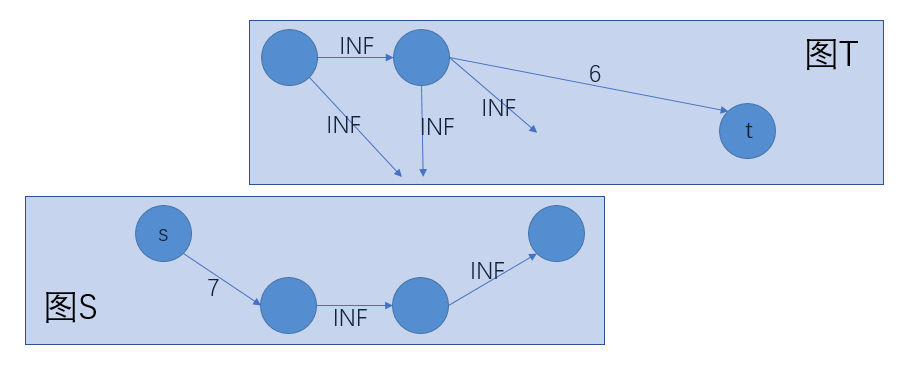
• 该图中的每一个简单割产生的两个子图，我们记含有点 s 的是图 S，含有点 t 的是图 T，则图 S 是最大权闭合子图。

简单割内不包含边权为 INF 的边，即不含有连通两个图的边（除了连接在 t 点上的边之外）；即，图 S 中没有边与图 T 连通，那么，所有的边都只能连接在图 S 之内，即为闭合图。

记割集中，所有连接在 s 上的边的权值和为 $x_1$，所有连接在 t 上的边的权值和为 $x_2$，则割集中所有边权值和为 $x=x_1+x_2$。

记图 S 中所有点的权值和为 $w$，记其中正权值之和为 $w_1$，负权值之和为 $- w_2$，故 $w = w_1 - w_2$。

因此，
$$
w+x=w_1-w_2+x_1-x_2
$$
又，
$$
x_2 = w_2
$$
因为图 S 中所有负权值的点必然连接到 t 点，而图 S 必然要与 t 分割开，故割集中，连接在 t 点上的边权值和就是图S中所有负权值点的权值之和取负。因而，
$$
w+x=w_1+x_1
$$
显然，$w_1 + x_1$ 是整个图中所有正权值之和，记为 $sum$，则
$$
w=sum-x
$$
即，图 S 中所有点的权值和 = 整个图中所有正权值之和 - 割集中所有边权值和。因为 $sum$ 为定值，只要我们取最小割，则图 S 中所有点的权值和就是最大的，即此时图 S 为最大权闭合子图。

栗子

　　　　　

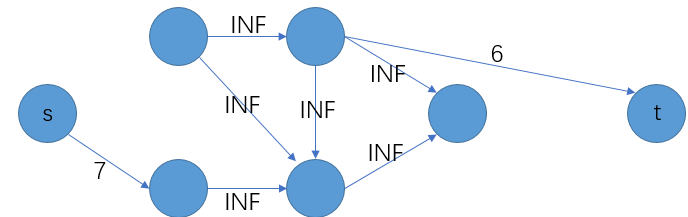
解法

• 先记录整个图中，所有正点权值的和；

• 建立对应流网络，求最大流，最大流在数值上等于最小割，故我们得到了流网络的 s-t 最小割；

• 所有正点权值的和减去 s-t 最小割，即得最大权闭合子图的权值和。

P2762 太空飞行计划问题

Hint

这里大概讲一下转换成最大流以后怎么输出。

一个结论就是假如我们跑的是 Dinic 那么我们最后一次网络流（这一次网络流并没有起任何作用，只是确认了无更多残余流量可以退出了）中，所有被分到层的都一定被选上了。

没有更多残余流量其实意味着这个图已经被割成了两部分，一个实验如果有层数意味着它没有被割掉（被选上了），一个仪器如果有层数意味着它已经被割掉了（也是被选上了）。

于是只要在最后输出所有有层数的点就行了。

Code

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <queue>
using namespace std;

const int N = 110, INF = 0x3f3f3f3f;
char tools[10000];

class node {
    public:
        int u, v, w, next;
} e[N * N];

int head[N], cur[N], tot = 0;

void add(int u, int v, int w) {
    e[tot] = {u, v, w, head[u]};
    head[u] = tot++;
    e[tot] = {v, u, 0, head[v]};
    head[v] = tot++;
}

int h[N], n, m, s, t;
bool bfs() {
    
    memset(h, 0, sizeof h);
    memcpy(cur, head, sizeof cur);
    
    queue<int> q;
    q.push(s);
    h[s] = 1;
    
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i = head[u]; i != -1; i = e[i].next) {
            int v = e[i].v;
            if(e[i].w and h[v] == 0) {
                h[v] = h[u] + 1;
                if(v == t) return true;
                q.push(v);
            }
        }
    }
    
    return false;
}

int dfs(int u, int low) {
    if(u == t) return low;
    int w = low;
    for(int i = cur[u]; i != -1; i = e[i].next, cur[u] = i) {
        int v = e[i].v;
        if(e[i].w and h[v] == h[u] + 1) {
            int f = dfs(v, min(w, e[i].w));
            if(f == 0) h[v] = 0;
            e[i].w -= f;
            e[i^1].w += f;
            w -= f;
            if(w == 0) break;
        }
    }
    return low - w;
}
int maxflow = 0, sum = 0;
void dinic() {
    int flow;
    while(bfs()) while(flow = dfs(s, INF)) maxflow += flow;
}
int main() {
    
    //freopen("shut2.in", "r", stdin);
    
    scanf("%d%d", &m, &n);
    
    memset(head, -1, sizeof head);
    s = 0, t = n+m+1;
    for(int i=1, w; i<=m; ++i) {
        
        scanf("%d", &w);
        add(s, i, w);
        sum += w;
        
        memset(tools, '\0', sizeof tools); 
        cin.getline(tools, 10000);
        int ulen = 0, tool;
        while(sscanf(tools + ulen, "%d", &tool) == 1) {
            add(i, tool + m, INF);
            if(tool == 0) ulen++;
            else {
                while(tool) {
                    tool /= 10;
                    ulen++;
                }
            }
            ulen++;
        }
    }
    
    for(int i=1, w; i<=n; ++i) {
        scanf("%d", &w);
        add(i+m, t, w);
    }
    
    dinic();
    
    for(int i=1; i<=m; ++i) if(h[i]) printf("%d ", i);
    printf("\n");
    for(int i=1; i<=n; ++i) if(h[i+m]) printf("%d ", i);
    printf("\n");
    
    printf("%d\n", sum - maxflow);
    
    return 0;
}

全局最小割

可参考这篇文章。

Code (POJ 2914, 未优化版)

#include <stdio.h>
#include <string.h>
#include <iostream>
using namespace std;

const int N = 550;

int g[N][N];
int dis[N];
bool flag[N], vis[N];
int n, m, s, t;

int main() {
    
    while(scanf("%d%d", &n, &m) != EOF) {
        
        memset(g, 0, sizeof g);
        
        for(int i=1, a, b, c; i<=m; ++i) {
            scanf("%d%d%d", &a, &b, &c);
            ++a, ++b;
            g[a][b] += c; g[b][a] += c; 
        }
        
        int ans = 0x3f3f3f3f;
        memset(flag, false, sizeof flag);
        
        for(int o=1; o<n; ++o) {
            
            s = t = 0;
            
            memset(vis, false, sizeof vis);
            memset(dis, 0, sizeof dis); 
            
            for(int p=1; p<=n; ++p) {
                
                int v = -1;
                for(int i=1; i<=n; ++i) 
                    if(!flag[i] and !vis[i] and (v == -1 or dis[v] < dis[i]))
                        v = i;
                if(v == -1) break;
                
                vis[v] = true;
                
                s=t, t=v;
                for(int i=1; i<=n; ++i) 
                    if(!flag[i] and !vis[i]) 
                        dis[i] += g[t][i];
            }
            
            flag[t] = true;
            ans = min(ans, dis[t]);
            
            if(ans == 0) break;
            
            for(int i=1; i<=n; ++i) {
                if(flag[i]) continue;
                g[s][i] += g[t][i];
                g[i][s] += g[i][t];
            }
                
        }
        
        printf("%d\n", ans);
    } 
    
    return 0;
}