题意分析
操作最少的次数,构成有趣图,注意无重边,有向边。
- 操作分为加边和删边。
- 有趣图定义
- 有一个中心,满足此点有自环,且与其他结点有双向边。
- 除中心点外的结点,满足出度 = 入度 = 2。
算法分析
1、仔细分析有趣图的定义,发现如下性质:
- 中心的边数为 $(n-1)\times 2+1$,也就是它与其他结点要有双向边再加自己的一个自环,无重边所以构造中心点时不可能做删除操作,只能加边或不操作。
- 其他结点的出入度为 2,排除掉与中心点连接的双向边,其点的度一定为一进一出。
2、如何判断结点的度满足一进一出。
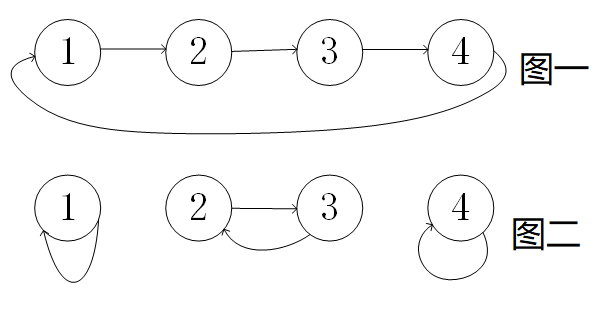
图一,图二都是满足结点度一进一出。所以 $n$ 个结点需要 $n$ 条相连边(首尾)。
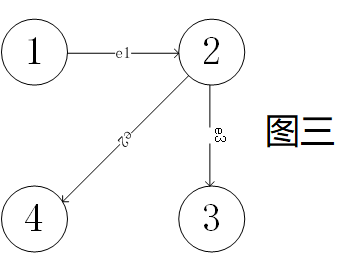
图三不满足,只有两条相连边 $(e_1,e_2)$ 或者选择 $(e_1,e_3)$ 即有用边,还需要添加 $n-2$ 边有用边,同时还要减掉 1 条边,即总边数减去有用边,也就是要删除的无用边。
方法1:拆点,一个点拆为进点和出点,建立二分图。
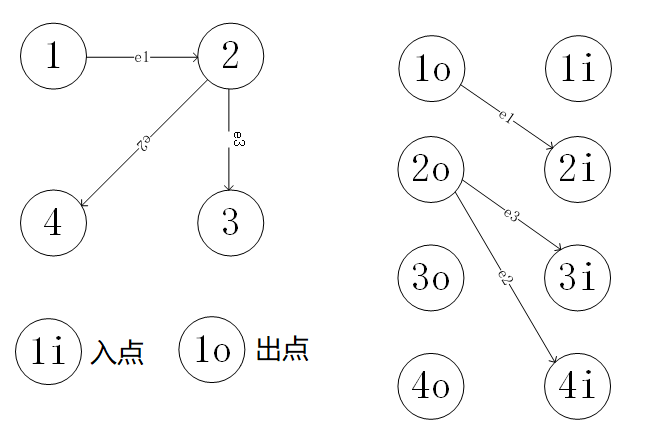
左边的点求匹配,最大匹配就是有用的边。
方法2:直接将图看成二分图,利用有向边每个点都求匹配。
3、枚举每个点做中心点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include <stdio.h>
#include <string.h>
#include <limits.h>
#include <vector>
#include <iostream>
using namespace std;
const int N = 550, INF = INT_MAX;
vector<int> g[N];
int c, n, m;
int tag = 0, vis[N], match[N];
bool mp[N][N];
bool dfs(int u) {
for(int i = 0; i < g[u].size(); ++i) {
int v = g[u][i];
if(v == c) continue;
if(vis[v] == tag) continue;
vis[v] = tag;
if(match[v] == 0 or dfs(match[v])) {
match[v] = u;
return true;
}
}
return false;
}
int best = INF;
int main() {
scanf("%d%d", &n, &m);
int sum0 = 0;
for(int i=1, u, v; i<=m; ++i) {
scanf("%d%d", &u, &v);
g[u].push_back(v);
mp[u][v] = true;
++sum0;
}
for(int i=1; i<=n; ++i) {
memset(match, 0, sizeof match);
c = i;
int ans = 0;
int sum1 = 0;
for(int j=1; j<=n; ++j) {
if(j == c) {
if(mp[c][c]) ++sum1;
continue;
}
if(mp[j][c]) ++sum1;
if(mp[c][j]) ++sum1;
}
ans += 2*(n-1) + 1 - sum1;
int sum2 = 0;
for(int j=1; j<=n; ++j) {
++tag;
if(j == c) continue;
if(dfs(j)) ++sum2;
}
ans += sum0 - sum1 - sum2 + n-1 - sum2;
best = min(best, ans);
}
printf("%d\n", best);
return 0;
}
|



